Publication

2026

1. PRL

   

   Entanglement Growth from Entangled States: A Unified Perspective on Entanglement Generation and Transport

   Chun-Yue Zhang, Zi-Xiang Li^†, and Shi-Xin Zhang^†

   Physical Review Letters, Jul 2026

   Abs Bib HTML PDF

   Studies of entanglement dynamics in quantum many-body systems have focused largely on initial product states. Here, we investigate the far richer dynamics from initial entangled states, uncovering universal patterns across diverse systems ranging from many-body localization (MBL) to random quantum circuits. Our central finding is that the growth of entanglement entropy can exhibit a counter-intuitive non-monotonic dependence on the initial entanglement in many non-ergodic systems, peaking for moderately entangled initial states. To understand this phenomenon, we introduce a conceptual framework that decomposes entanglement growth into two mechanisms: “build” and “move”. The “build” mechanism creates new entanglement, while the “move” mechanism redistributes pre-existing entanglement throughout the system. Specifically, we demonstrate that MBL dynamics are “move-dominated”, exhibiting a quantitative agreement with a random SWAP circuit that serves as a model of pure “move” dynamics by uniformly distributing pre-existing entanglement. This implies that MBL acts as a redistributor of a hidden entanglement reservoir quantified by the bipartition-averaged entropy. This “build-move” framework offers a unified perspective for classifying diverse physical dynamics, deepening our understanding of entanglement propagation and information processing in quantum many-body systems.

   @article{Zhang2026_growth,
     title = {Entanglement Growth from Entangled States: A Unified Perspective on Entanglement Generation and Transport},
     author = {Zhang, Chun-Yue and Li, Zi-Xiang and Zhang, Shi-Xin},
     journal = {Physical Review Letters},
     volume = {137},
     number = {2},
     pages = {020404},
     year = {2026},
     month = jul,
     doi = {10.1103/xkh7-gdqm},
     url = {https://journals.aps.org/prl/abstract/10.1103/xkh7-gdqm},
   }

2. PRX Quantum

   

   Intrinsic Preservation of Plasticity in Continual Quantum Learning

   Yu-Qin Chen^†, and Shi-Xin Zhang^†

   PRX Quantum, Jul 2026

   Abs Bib HTML PDF

   Artificial intelligence in dynamic, real-world environments requires the capacity for continual learning. However, standard deep learning suffers from a fundamental issue: loss of plasticity, in which networks gradually lose their ability to learn from new data. Here we show that quantum learning models naturally overcome this limitation, preserving plasticity over long timescales. We demonstrate this advantage systematically across a broad spectrum of tasks from multiple learning paradigms, including supervised learning and reinforcement learning, and diverse data modalities, from classical high-dimensional images to quantum-native datasets. Although classical models exhibit performance degradation correlated with unbounded weight and gradient growth, quantum neural networks maintain consistent learning capabilities regardless of the data or task. We identify the origin of the advantage as the intrinsic physical constraints of quantum models. Unlike classical networks where unbounded weight growth leads to landscape ruggedness or saturation, the unitary constraints confine the optimization to a compact manifold. Our results suggest that the utility of quantum computing in machine learning extends beyond potential speedups, offering a robust pathway for building adaptive artificial intelligence and lifelong learners.

   @article{Chen2026_plasticity,
     title = {Intrinsic Preservation of Plasticity in Continual Quantum Learning},
     author = {Chen, Yu-Qin and Zhang, Shi-Xin},
     journal = {PRX Quantum},
     volume = {7},
     number = {3},
     pages = {033003},
     year = {2026},
     month = jul,
     doi = {10.1103/ry52-85ll},
     url = {https://journals.aps.org/prxquantum/abstract/10.1103/ry52-85ll},
   }

3. Nat. Commun.

   

   Superior resilience to poisoning and amenability to unlearning in quantum machine learning

   Yu-Qin Chen^†, and Shi-Xin Zhang^†

   Nature Communications, Mar 2026

   Abs Bib HTML PDF

   The reliability of artificial intelligence hinges on the integrity of its training data, a foundation often compromised by noise and corruption. Here, through a comparative study of classical and quantum neural networks on both classical and quantum data, we reveal a fundamental difference in their response to data corruption. We find that classical models exhibit brittle memorization, leading to a failure in generalization. In contrast, quantum models demonstrate superior resilience, underscored by a phase transition-like response to increasing noise, revealing a critical point beyond which the model’s performance changes qualitatively. We further introduce a framework of quantum machine unlearning, the process of efficiently forcing a trained model to forget bad influences. We show that classical models form rigid, stubborn memories of erroneous data, while the quantum model is significantly more amenable to efficient forgetting with approximate unlearning methods. Our findings establish that quantum machine learning possesses the dual advantage of intrinsic resilience and efficient adaptability, providing a promising paradigm for the trustworthy and reliable artificial intelligence of the future.

   @article{Chen_2026,
     title = {Superior resilience to poisoning and amenability to unlearning in quantum machine learning},
     author = {Chen, Yu-Qin and Zhang, Shi-Xin},
     journal = {Nature Communications},
     volume = {17},
     number = {3716},
     year = {2026},
     month = mar,
     doi = {10.1038/s41467-026-70420-4},
     url = {https://www.nature.com/articles/s41467-026-70420-4},
     issn = {2041-1723},
   }

4. PRL

   Imaginary-Time Mpemba Effect in Quantum Many-Body Systems

   Wei-Xuan Chang, Shuai Yin, Shi-Xin Zhang^†, and Zi-Xiang Li^†

   Physical Review Letters, Mar 2026

   Abs Bib HTML

   Various exotic phenomena emerge in nonequilibrium quantum many-body systems. The Mpemba effect, denoting the situation where a hot system freezes faster than a colder one, is a counterintuitive nonequilibrium phenomenon that has attracted enduring interest for more than half a century. In this Letter, we unveil a novel phenomenon of the Mpemba effect in the imaginary-time relaxation dynamics in quantum many-body systems, termed as the imaginary-time Mpemba effect (ITME). We propose a mechanism for the ITME rooted in the initial state’s eigenbasis expansion, and we demonstrate its emergence in representative quantum lattice models. Using sign-free quantum Monte Carlo (QMC) simulations, we unequivocally establish the existence of the ITME across diverse interacting quantum systems. Crucially, given the widespread use of imaginary-time dynamics for ground-state calculations, the discovery of the ITME potentially provides a new pathway to accelerate quantum many-body simulations, particularly for QMC methods hindered by the sign problem.

   @article{Chang_2026,
     title = {Imaginary-Time Mpemba Effect in Quantum Many-Body Systems},
     author = {Chang, Wei-Xuan and Yin, Shuai and Zhang, Shi-Xin and Li, Zi-Xiang},
     journal = {Physical Review Letters},
     volume = {136},
     number = {10},
     year = {2026},
     month = mar,
     doi = {10.1103/dvrt-n2hq},
     url = {https://journals.aps.org/prl/abstract/10.1103/dvrt-n2hq},
     issn = {1079-7114},
   }

2025

1. Sci. Bull.

   

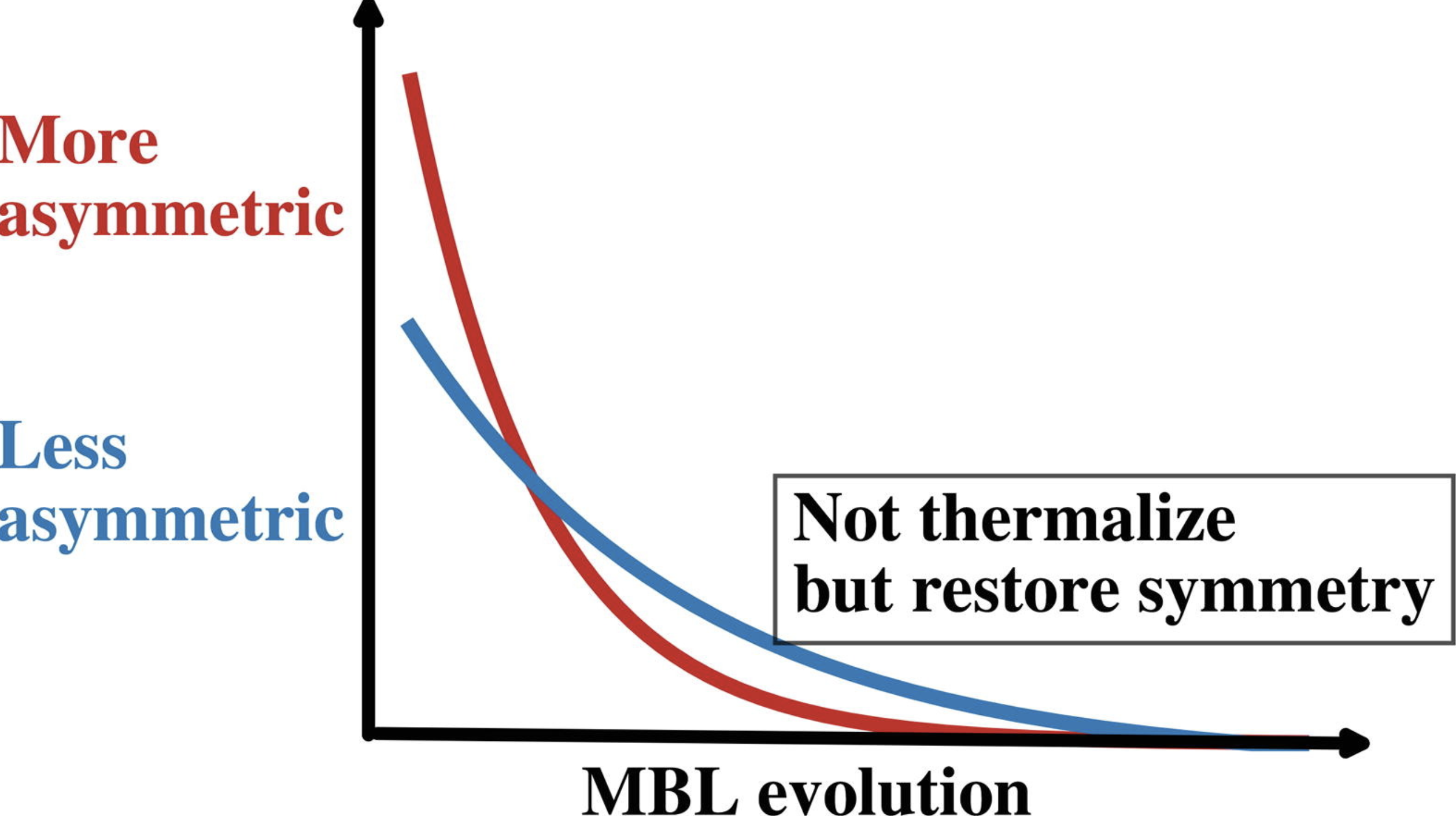   Symmetry restoration and quantum Mpemba effect in many-body localization systems

   Shuo Liu , Hao-Kai Zhang, Shuai Yin, Shi-Xin Zhang^†, and Hong Yao^†

   Science Bulletin, Dec 2025

   Abs Bib HTML PDF

   Non-equilibrium dynamics of quantum many-body systems has attracted increasing attention owing to a variety of intriguing phenomena absent in equilibrium physics. A prominent example is the quantum Mpemba effect, where subsystem symmetry is restored more rapidly under a symmetric quench from a more asymmetric initial state. In this work, we investigate symmetry restoration and the quantum Mpemba effect in many-body localized systems for a range of initial states. We show that symmetry can still be restored in the many-body localization regime without approaching thermal equilibrium. Moreover, we demonstrate that the quantum Mpemba effect emerges universally for any tilted product state, in contrast to chaotic systems where its occurrence depends sensitively on the choice of the initial state. We further provide a theoretical analysis of symmetry restoration and the quantum Mpemba effect using an effective model for many-body localization. Overall, this paper fills an important gap in establishing a unified understanding of symmetry restoration and the quantum Mpemba effect in generic many-body systems, and it advances our understanding of many-body localization.

   @article{LIU20253991,
     title = {Symmetry restoration and quantum Mpemba effect in many-body localization systems},
     journal = {Science Bulletin},
     volume = {70},
     number = {23},
     pages = {3991-3996},
     year = {2025},
     month = dec,
     issn = {2095-9273},
     doi = {10.1016/j.scib.2025.10.017},
     url = {https://www.sciencedirect.com/science/article/pii/S2095927325010394},
     author = {Liu, Shuo and Zhang, Hao-Kai and Yin, Shuai and Zhang, Shi-Xin and Yao, Hong},
   }

2. CPL

   Symmetry Breaking Dynamics in Quantum Many-Body Systems

   Hui Yu, Zi-Xiang Li^†, and Shi-Xin Zhang^†

   Chin. Phys. Lett., Nov 2025

   Abs Bib HTML PDF

   Entanglement asymmetry (EA) has emerged as a powerful tool for characterizing symmetry breaking in quantum many-body systems. In this Letter, we explore how symmetry is dynamically broken through the lens of EA in two distinct scenarios: a non-symmetric Hamiltonian quench and a non-symmetric random quantum circuit, with a particular focus on U(1) symmetry. In the former case, symmetry remains broken in the subsystem at late times, whereas in the latter case, the symmetry is initially broken and subsequently restored, consistent with the principles of quantum thermalization. Notably, the growth of EA exhibits unexpected overshooting behavior at early times in both contexts, contrasting with the behavior of charge variance. We also consider dynamics of non-symmetric initial states under the symmetry-breaking evolution. Due to the competition of symmetry-breaking in both the initial state and Hamiltonian, the early-time EA can increase and decrease, while quantum Mpemba effects remain evident despite the weak symmetry-breaking in both settings.

   @article{cpl_42_11_110602,
     title = {Symmetry Breaking Dynamics in Quantum Many-Body Systems},
     journal = {Chin. Phys. Lett.},
     volume = {42},
     number = {11},
     pages = {110602},
     year = {2025},
     month = nov,
     doi = {10.1088/0256-307X/42/11/110602},
     url = {http://cpl.iphy.ac.cn/en/article/doi/10.1088/0256-307X/42/11/110602},
     author = {Yu, Hui and Li, Zi-Xiang and Zhang, Shi-Xin},
   }

3. PRR

   Effective temperature in approximate quantum many-body states

   Yu-Qin Chen^†, and Shi-Xin Zhang^†

   Physical Review Research, Aug 2025

   Abs Bib HTML PDF

   In the pursuit of numerically identifying ground states of quantum many-body systems, approximate quantum wave function ansatzes are commonly employed. This study focuses on the spectral decomposition of these approximate quantum many-body states into exact eigenstates of the target Hamiltonian, which reflects the intricate physics at the interplay between quantum systems and numerical algorithms. Here, we examine various parametrized approximate quantum states constructed from neural networks, tensor networks, and quantum circuits, employing differentiable programming to numerically approximate ground states and imaginary-time evolved states. Our findings reveal a consistent exponential pattern in the energy eigenbasis decomposition contributions of approximate states across different ansatzes, optimization objectives, and quantum systems, characterized by remarkably small decay rates, i.e., high effective temperatures. This finding is counterintuitive for high-fidelity approximate ground states: While the total contribution from excited states can be made sufficiently small, the residual spectral weight does not decay rapidly with energy. This behavior is an intrinsic property of the variational ansatz, independent of the approximation’s overall accuracy. The effective temperature is related to ansatz expressiveness and accuracy and shows phase transition behaviors in learning imaginary-time evolved states. The universal picture and unique features suggest the significance and potential of the effective temperature metric in characterizing approximate quantum states.

   @article{chen2025et,
     author = {Chen, Yu-Qin and Zhang, Shi-Xin},
     doi = {10.1103/zpjv-bm5c},
     journal = {Physical Review Research},
     month = aug,
     pages = {033185},
     title = {Effective temperature in approximate quantum many-body states},
     volume = {7},
     year = {2025},
   }

4. AAPPS

   

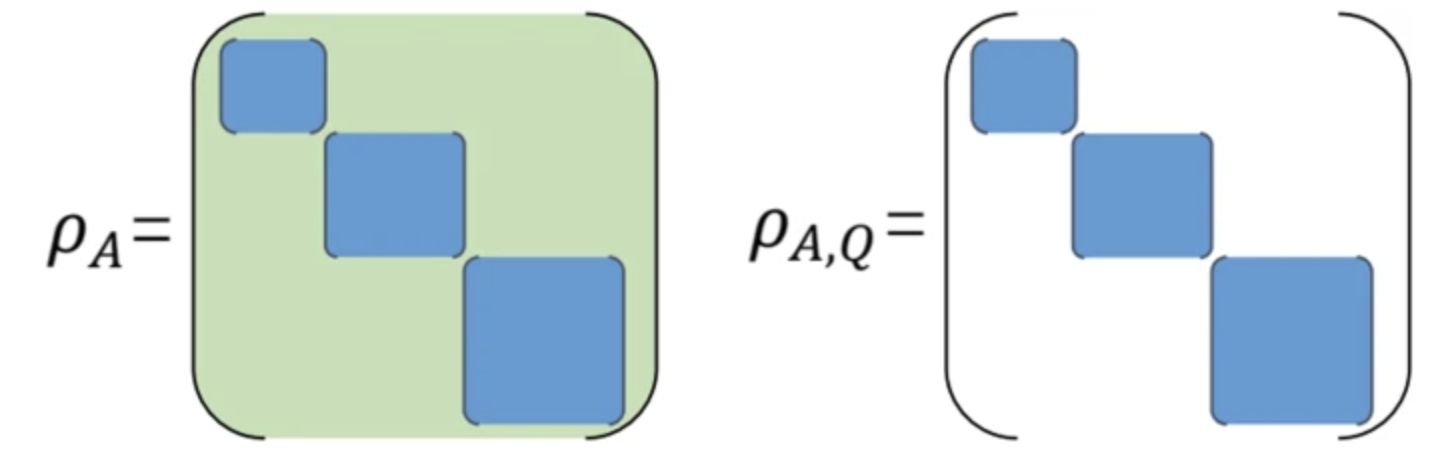   Quantum Mpemba effects from symmetry perspectives

   Hui Yu, Shuo Liu, and Shi-Xin Zhang^†

   AAPPS Bulletin, Jul 2025

   Abs Bib HTML PDF

   Non-equilibrium dynamics have become a central research focus, exemplified by the counterintuitive Mpemba effect where initially hotter systems can cool faster than colder ones. Studied extensively in both classical and quantum regimes, this phenomenon reveals diverse and complex behaviors across different systems. This review provides a concise overview of the quantum Mpemba effect (QME), specifically emphasizing its connection to symmetry breaking and restoration in closed quantum many-body systems. We begin by outlining the classical Mpemba effect and its quantum counterparts, summarizing key findings. Subsequently, we introduce entanglement asymmetry and charge variance as key metrics for probing the QME from symmetry perspectives. Leveraging these tools, we analyze the early- and late-time dynamics of these quantities under Hamiltonian evolution and random unitary circuits. We conclude by discussing significant challenges and promising avenues for future research.

   @article{Yu2025_review,
     author = {Yu, Hui and Liu, Shuo and Zhang, Shi-Xin},
     doi = {10.1007/s43673-025-00157-7},
     issn = {2309-4710},
     issue = {1},
     journal = {AAPPS Bulletin},
     month = jul,
     pages = {17},
     title = {Quantum Mpemba effects from symmetry perspectives},
     volume = {35},
     year = {2025},
   }

5. Quantum

   

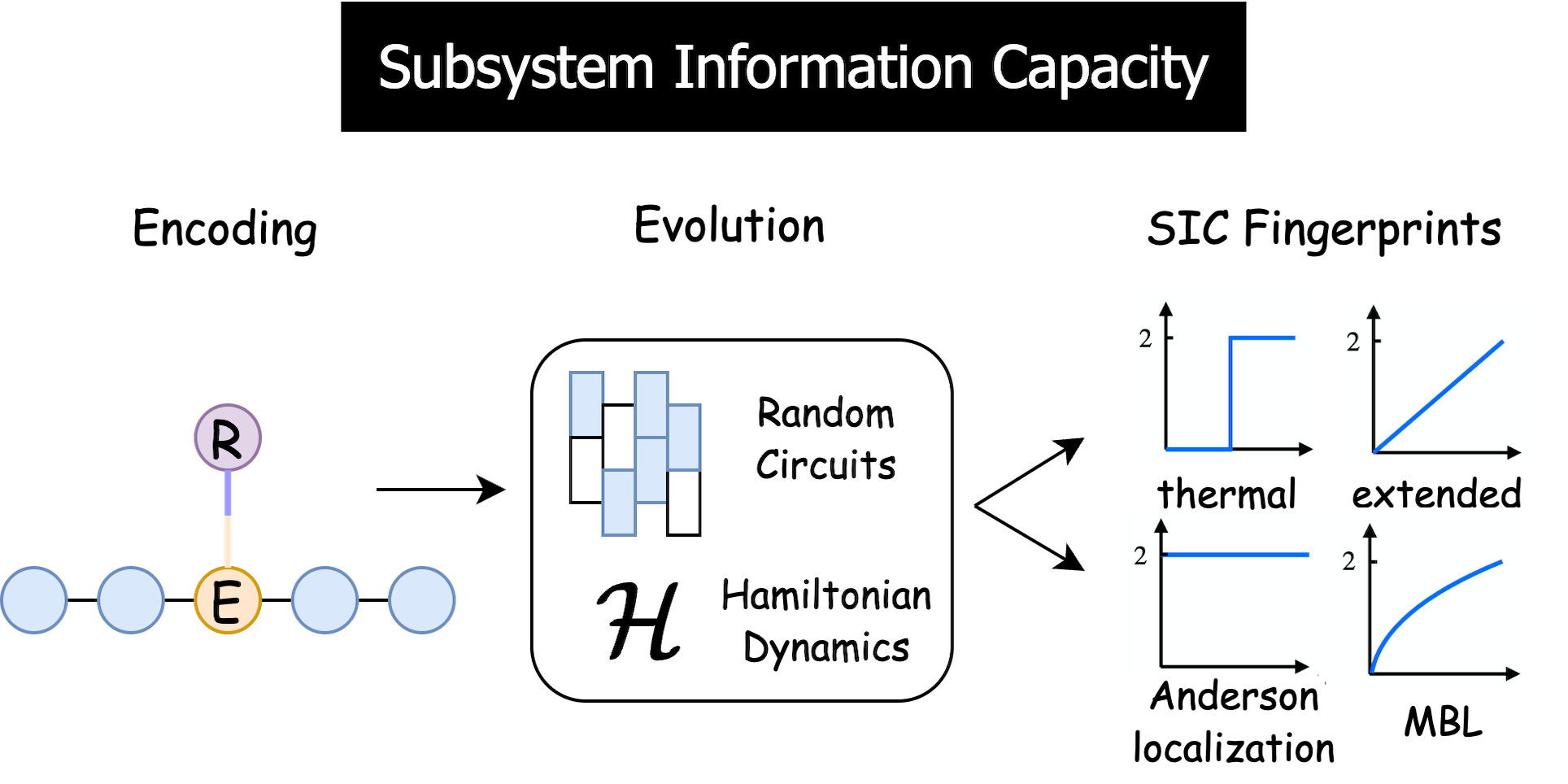   Subsystem Information Capacity in Random Circuits and Hamiltonian Dynamics

   Yu-Qin Chen, Shuo Liu, and Shi-Xin Zhang^†

   Quantum, Jun 2025

   Abs Bib HTML PDF

   In this study, we explore the information capacity of open quantum systems, focusing on the effective channels formed by the subsystem of random quantum circuits and quantum Hamiltonian evolution. By analyzing the subsystem information capacity, which is closely linked to quantum coherent information of these effective quantum channels, we uncover a diverse range of dynamical and steady behaviors depending on the types of evolution. Therefore, the subsystem information capacity serves as a valuable tool for studying the intrinsic nature of various dynamical phases, such as integrable, localized, thermalized, and topological systems. We also reveal the impact of different initial information encoding schemes on information dynamics including one-to-one, one-to-many, and many-to-many. To support our findings, we provide representative examples for numerical simulations, including random quantum circuits with or without mid-circuit measurements, random Clifford Floquet circuits, free and interacting Aubry-André models, and Su-Schrieffer-Heeger models. These numerical results are further quantitatively explained using the effective statistical model mapping and the quasiparticle picture in the cases of random circuits and non-interacting Hamiltonian dynamics, respectively.

   @article{chen2024subsystem,
     author = {Chen, Yu-Qin and Liu, Shuo and Zhang, Shi-Xin},
     doi = {10.22331/q-2025-06-24-1783},
     issn = {2521-327X},
     journal = {Quantum},
     month = jun,
     pages = {1783},
     title = {Subsystem Information Capacity in Random Circuits and Hamiltonian Dynamics},
     volume = {9},
     year = {2025},
     url = {https://doi.org/10.22331/q-2025-06-24-1783},
   }

2024

1. PRL

   

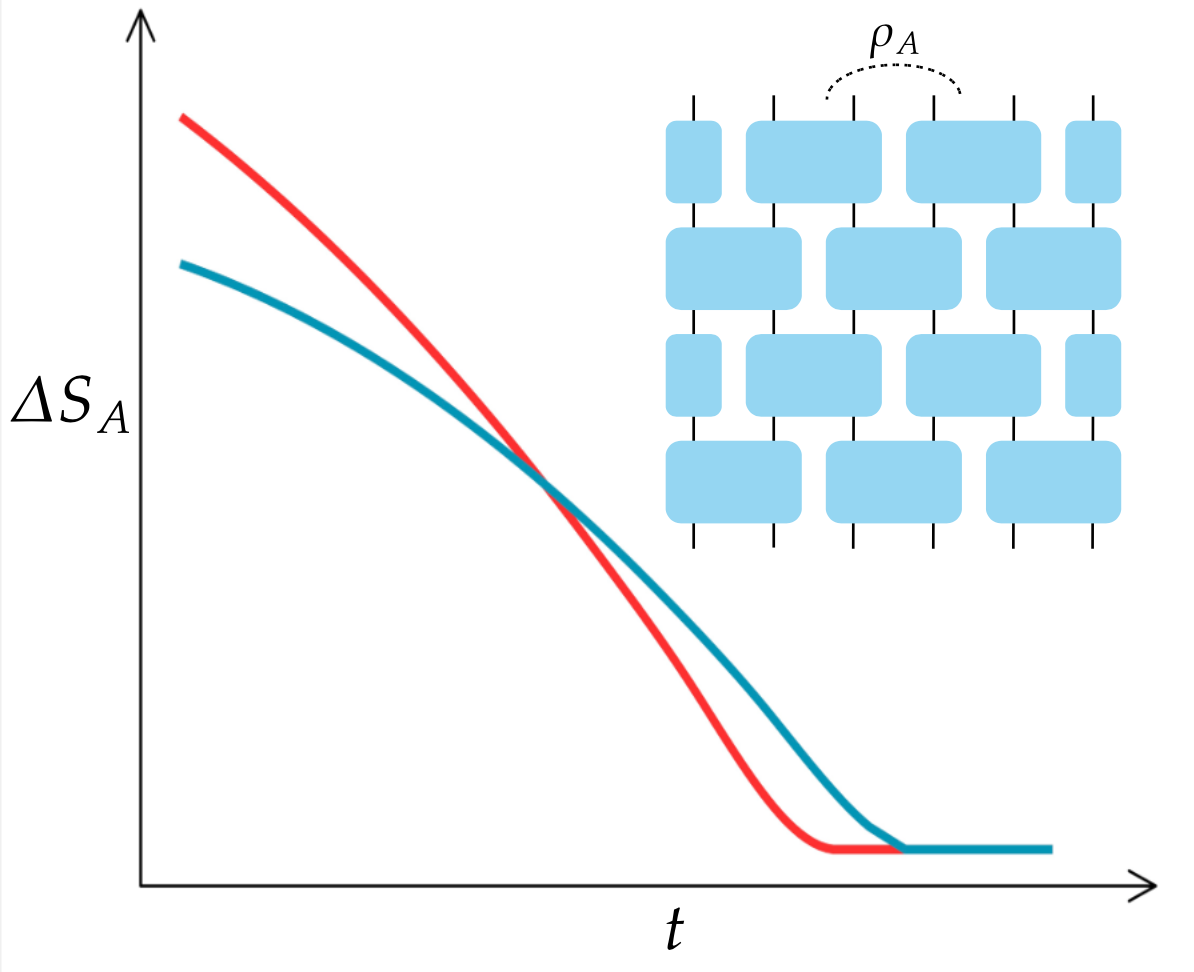   Symmetry Restoration and Quantum Mpemba Effect in Symmetric Random Circuits

   Shuo Liu , Hao-Kai Zhang, Shuai Yin, and Shi-Xin Zhang^†

   Phys. Rev. Lett., Oct 2024

   Abs Bib HTML PDF

   Entanglement asymmetry, which serves as a diagnostic tool for symmetry breaking and a proxy for thermalization, has recently been proposed and studied in the context of symmetry restoration for quantum many-body systems undergoing a quench. In this Letter, we investigate symmetry restoration in various symmetric random quantum circuits, particularly focusing on the U(1) symmetry case. In contrast to nonsymmetric random circuits where the U(1) symmetry of a small subsystem can always be restored at late times, we reveal that symmetry restoration can fail in U(1)-symmetric circuits for certain weak symmetry-broken initial states in finite-size systems. In the early-time dynamics, we observe an intriguing quantum Mpemba effect implying that symmetry is restored faster when the initial state is more asymmetric. Furthermore, we also investigate the entanglement asymmetry dynamics for SU(2) and ?2 symmetric circuits and identify the presence and absence of the quantum Mpemba effect for the corresponding symmetries, respectively. A unified understanding of these results is provided through the lens of quantum thermalization with conserved charges.

   @article{Liu2024_mpemba,
     author = {Liu, Shuo and Zhang, Hao-Kai and Yin, Shuai and Zhang, Shi-Xin},
     doi = {10.1103/PhysRevLett.133.140405},
     issn = {0031-9007},
     journal = {Phys. Rev. Lett.},
     month = oct,
     number = {14},
     pages = {140405},
     title = {{Symmetry Restoration and Quantum Mpemba Effect in Symmetric Random Circuits}},
     url = {https://link.aps.org/doi/10.1103/PhysRevLett.133.140405},
     volume = {133},
     year = {2024},
   }

2. PRApplied

   Exploring the topological sector optimization on quantum computers

   Yi-Ming Ding^†, Yan-Cheng Wang, Shi-Xin Zhang^†, and Zheng Yan^†

   Phys. Rev. Appl., Sep 2024

   Abs Bib HTML PDF

   Optimization problems are the core challenge in many fields of science and engineering, yet general and effective methods are scarce for searching optimal solutions. Quantum computing has been envisioned to help solve such problems, for example, the quantum annealing (QA) method based on adiabatic evolution has been extensively explored and successfully implemented on quantum simulators such as D-wave’s annealers and some Rydberg arrays. In this work, we investigate topological sector optimization (TSO) problem, which attracts particular interests in the quantum many-body physics community. We reveal that the topology induced by frustration in the spin model is an intrinsic obstruction for QA and other traditional methods to approach the ground state. We demonstrate that the optimization difficulties of TSO problem are not restricted to the gaplessness, but are also due to the topological nature which are often ignored for the analysis of optimization problems before. To solve TSO problems, we utilize quantum imaginary time evolution (QITE) with a possible realization on quantum computers, which exploits the property of quantum superposition to explore the full Hilbert space and can thus address optimization problems of topological nature. We report the performance of different quantum optimization algorithms on TSO problems and demonstrate that their capability to address optimization problems are distinct even when considering the quantum computational resources required for practical QITE implementations.

   @article{Ding2023,
     archiveprefix = {arXiv},
     arxivid = {2310.04291},
     author = {Ding, Yi-Ming and Wang, Yan-Cheng and Zhang, Shi-Xin and Yan, Zheng},
     doi = {10.1103/PhysRevApplied.22.034031},
     eprint = {2310.04291},
     issn = {2331-7019},
     journal = {Phys. Rev. Appl.},
     month = sep,
     number = {3},
     pages = {034031},
     title = {{Exploring the topological sector optimization on quantum computers}},
     url = {https://link.aps.org/doi/10.1103/PhysRevApplied.22.034031},
     volume = {22},
     year = {2024},
   }

3. PRB

   Noise-induced phase transitions in hybrid quantum circuits

   Shuo Liu , Ming-Rui Li, Shi-Xin Zhang^†, Shao-Kai Jian^†, and Hong Yao^†

   Phys. Rev. B, Aug 2024

   Abs Bib HTML PDF

   The presence of quantum noises inherent to real physical systems can strongly impact the physics in hybrid quantum circuits with local random unitaries and midcircuit measurements. The quantum noises with a size-independent occurring probability can lead to the disappearance of a measurement-induced entanglement phase transition and the emergence of a single area-law phase. In this work, we investigate the effects of quantum noises with size-dependent probabilities 𝑞=𝑝/𝐿𝛼, where 𝛼 represents the scaling exponent. We have identified a noise-induced entanglement phase transition from a volume law to a power (area) law in the presence (absence) of measurements as 𝑝 increases when 𝛼=1. With the help of an effective statistical model, we reveal that the phase transition is of first order arising from the competition between two types of spin configurations and shares the same analytical understanding as the noise-induced coding transition. This unified picture further deepens the understanding of the connection between entanglement behavior and the capacity of information protection. When 𝛼≠1, one spin configuration always dominates regardless of 𝑝 and thus the phase transition disappears. Moreover, we highlight the difference between the effects of size-dependent bulk noise and boundary noises. We validate our analytical predictions with extensive numerical results from stabilizer circuit simulations.

   @article{Liu2024_MIPT2,
     author = {Liu, Shuo and Li, Ming-Rui and Zhang, Shi-Xin and Jian, Shao-Kai and Yao, Hong},
     doi = {10.1103/PhysRevB.110.064323},
     issn = {2469-9950},
     journal = {Phys. Rev. B},
     month = aug,
     number = {6},
     pages = {064323},
     title = {{Noise-induced phase transitions in hybrid quantum circuits}},
     url = {https://link.aps.org/doi/10.1103/PhysRevB.110.064323},
     volume = {110},
     year = {2024}
   }

4. PRL

   

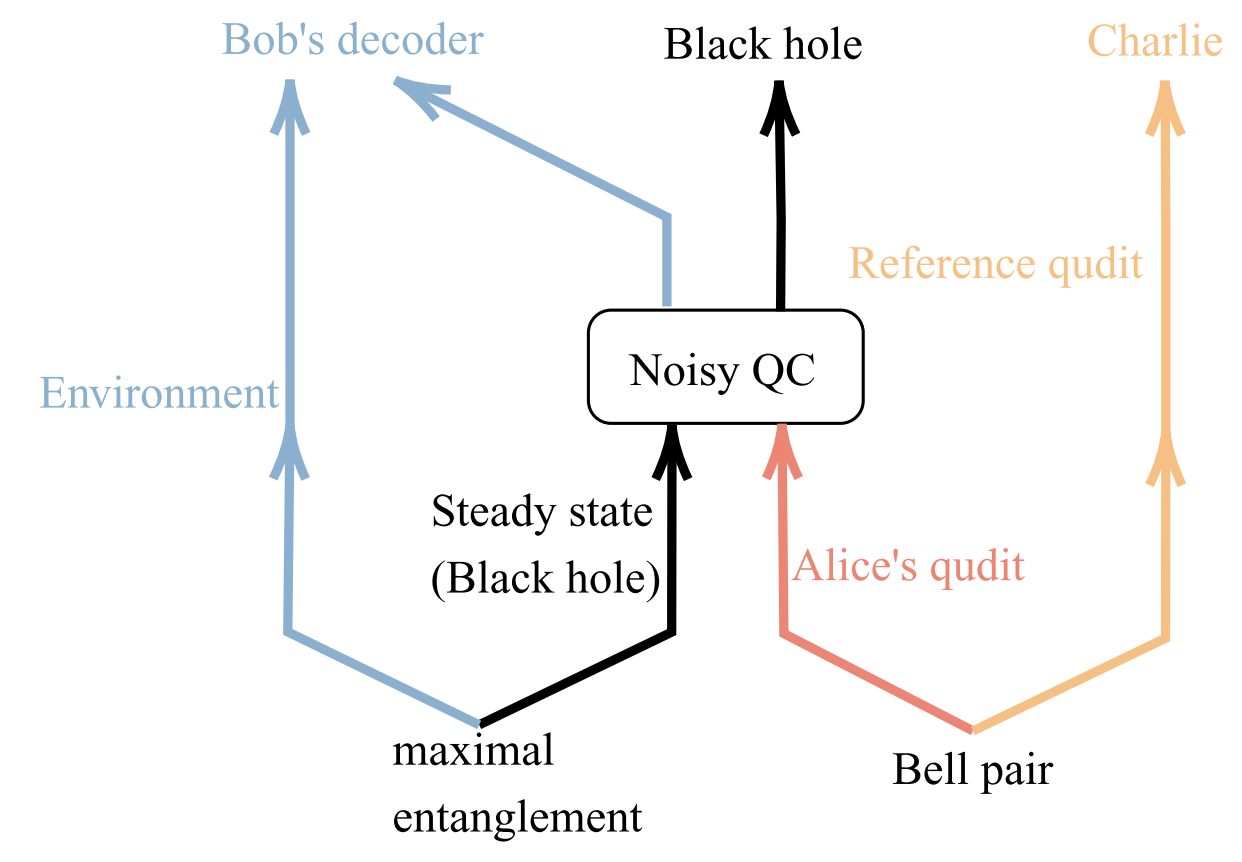   Entanglement Structure and Information Protection in Noisy Hybrid Quantum Circuits

   Shuo Liu , Ming-Rui Li, Shi-Xin Zhang^†, and Shao-Kai Jian^†

   Phys. Rev. Lett., Jun 2024

   Abs Bib HTML PDF

   In the context of measurement-induced entanglement phase transitions, the influence of quantum noises, which are inherent in real physical systems, is of great importance and experimental relevance. In this Letter, we present a comprehensive theoretical analysis of the effects of both temporally uncorrelated and correlated quantum noises on entanglement generation and information protection. This investigation reveals that entanglement within the system follows q^-1/3 scaling for both types of quantum noises, where q represents the noise probability. The scaling arises from the Kardar-Parisi-Zhang fluctuation with effective length scale L_\texteff ∼q^-1. More importantly, the information protection timescales of the steady states are explored and shown to follow q^-1/2 and q^-2/3 scaling for temporally uncorrelated and correlated noises, respectively. The former scaling can be interpreted as a Hayden-Preskill protocol, while the latter is a direct consequence of Kardar-Parisi-Zhang fluctuations. We conduct extensive numerical simulations using stabilizer formalism to support the theoretical understanding. This Letter not only contributes to a deeper understanding of the interplay between quantum noises and measurement-induced phase transition but also provides a new perspective to understand the effects of Markovian and non-Markovian noises on quantum computation.

   @article{Liu2024_MIPT1,
     archiveprefix = {arXiv},
     arxivid = {2401.01593},
     author = {Liu, Shuo and Li, Ming-Rui and Zhang, Shi-Xin and Jian, Shao-Kai},
     doi = {10.1103/PhysRevLett.132.240402},
     eprint = {2401.01593},
     issn = {0031-9007},
     journal = {Phys. Rev. Lett.},
     month = jun,
     number = {24},
     pages = {240402},
     title = {{Entanglement Structure and Information Protection in Noisy Hybrid Quantum Circuits}},
     url = {https://link.aps.org/doi/10.1103/PhysRevLett.132.240402},
     volume = {132},
     year = {2024},
   }

5. Comm Phys

   Quantum approximate optimization via learning-based adaptive optimization

   Lixue Cheng^†, Yu-Qin Chen, Shi-Xin Zhang^† , and Shengyu Zhang^†

   Communications Physics, Mar 2024

   Abs Bib HTML PDF

   Combinatorial optimization problems are ubiquitous and computationally hard to solve in general. Quantum approximate optimization algorithm (QAOA), one of the most representative quantum-classical hybrid algorithms, is designed to solve combinatorial optimization problems by transforming the discrete optimization problem into a classical optimization problem over continuous circuit parameters. QAOA objective landscape is notorious for pervasive local minima, and its viability significantly relies on the efficacy of the classical optimizer. In this work, we design double adaptive-region Bayesian optimization (DARBO) for QAOA. Our numerical results demonstrate that the algorithm greatly outperforms conventional optimizers in terms of speed, accuracy, and stability. We also address the issues of measurement efficiency and the suppression of quantum noise by conducting the full optimization loop on a superconducting quantum processor as a proof of concept. This work helps to unlock the full power of QAOA and paves the way toward achieving quantum advantage in practical classical tasks.

   @article{Cheng2024,
     author = {Cheng, Lixue and Chen, Yu-Qin and Zhang, Shi-Xin and Zhang, Shengyu},
     doi = {10.1038/s42005-024-01577-x},
     issn = {2399-3650},
     journal = {Communications Physics},
     month = mar,
     number = {1},
     pages = {83},
     title = {{Quantum approximate optimization via learning-based adaptive optimization}},
     url = {https://www.nature.com/articles/s42005-024-01577-x},
     volume = {7},
     year = {2024},
   }

6. PRApplied

   Neural-network-encoded variational quantum algorithms

   Jiaqi Miao, Chang-Yu Hsieh^†, and Shi-Xin Zhang^†

   Phys. Rev. Appl., Jan 2024

   Abs Bib HTML PDF

   We introduce a general framework called neural-network- (NN) encoded variational quantum algorithms (VQAs), or NNVQA for short, to address the challenges of implementing VQAs on noisy intermediate-scale quantum (NISQ) computers. Specifically, NNVQA feeds input (such as parameters of a Hamiltonian) from a given problem to a neural network and uses its outputs to parameterize an ansatz circuit for the standard VQA. Combining the strengths of NN and parameterized quantum circuits, NNVQA can accelerate the training process of VQAs and handle a broad family of related problems with varying input parameters with the pretrained NN. To concretely illustrate the merits of NNVQA, we present results on a NN variational quantum eigensolver (VQE) for solving the ground state of parameterized ?⁢?⁢? spin models in one and two dimensions. Our results demonstrate that NNVQE is able to estimate the ground-state energies of parameterized Hamiltonians with high precision without fine tuning, and significantly reduce the overall training cost to estimate ground-state properties across the phases of the given Hamiltonian. We also employ an active learning strategy to further increase the training efficiency while maintaining prediction accuracy. These encouraging results demonstrate that NNVQAs offer an alternative hybrid quantum-classical paradigm to utilize NISQ resources for solving more realistic and challenging computational problems.

   @article{Miao2024,
     author = {Miao, Jiaqi and Hsieh, Chang-Yu and Zhang, Shi-Xin},
     doi = {10.1103/PhysRevApplied.21.014053},
     issn = {2331-7019},
     journal = {Phys. Rev. Appl.},
     month = jan,
     number = {1},
     pages = {014053},
     title = {{Neural-network-encoded variational quantum algorithms}},
     url = {https://link.aps.org/doi/10.1103/PhysRevApplied.21.014053},
     volume = {21},
     year = {2024},
   }

2023

1. PRR

   Training variational quantum algorithms with random gate activation

   Shuo Liu, Shi-Xin Zhang^†, Shao-Kai Jian^†, and Hong Yao^†

   Phys. Rev. Res., Sep 2023

   Abs Bib HTML PDF

   Variational quantum algorithms (VQAs) hold great potentials for near-term applications and are promising to achieve quantum advantage on practical tasks. However, VQAs suffer from severe barren plateau problem as well as have a large probability of being trapped in local minima. In this Letter, we propose a novel training algorithm with random quantum gate activation for VQAs to efficiently address these two issues. This new algorithm processes effectively much fewer training parameters than the conventional plain optimization strategy, which efficiently mitigates barren plateaus with the same expressive capability. Additionally, by randomly adding two-qubit gates to the circuit ansatz, the optimization trajectories can escape from local minima and reach the global minimum more frequently due to more sources of randomness. In real quantum experiments, the new training algorithm can also reduce the quantum computational resources required and be more quantum noise resilient. We apply our training algorithm to solve variational quantum simulation problems for ground states and present convincing results that showcase the advantages of our novel strategy where better performance is achieved by the combination of mitigating barren plateaus, escaping from local minima, and reducing the effect of quantum noises. We further propose that the entanglement phase transition could be one underlying reason why our RA training is so effective.

   @article{Liu2023_ra,
     archiveprefix = {arXiv},
     arxivid = {2303.08154},
     author = {Liu, Shuo and Zhang, Shi-Xin and Jian, Shao-Kai and Yao, Hong},
     doi = {10.1103/PhysRevResearch.5.L032040},
     eprint = {2303.08154},
     issn = {2643-1564},
     journal = {Phys. Rev. Res.},
     month = sep,
     number = {3},
     pages = {L032040},
     title = {{Training variational quantum algorithms with random gate activation}},
     url = {https://link.aps.org/doi/10.1103/PhysRevResearch.5.L032040},
     volume = {5},
     year = {2023},
   }

2. PRR

   Automatic differentiable Monte Carlo: Theory and application

   Shi-Xin Zhang, Zhou-Quan Wan, and Hong Yao^†

   Phys. Rev. Res., Jul 2023

   Abs Bib HTML PDF

   Differentiable programming has emerged as a key programming paradigm empowering rapid developments of deep learning while its applications to important computational methods such as Monte Carlo remain largely unexplored. Here we present the general theory enabling infinite-order automatic differentiation on expectations computed by Monte Carlo with unnormalized probability distributions, which we call "automatic differentiable Monte Carlo" (ADMC). By implementing ADMC algorithms on computational graphs, one can also leverage state-of-the-art machine learning frameworks and techniques to traditional Monte Carlo applications in statistics and physics. We illustrate the versatility of ADMC by showing some applications: fast search of phase transitions and accurately finding ground states of interacting many-body models in two dimensions. ADMC paves a promising way to innovate Monte Carlo in various aspects to achieve higher accuracy and efficiency, e.g. easing or solving the sign problem of quantum many-body models through ADMC.

   @article{Zhang2019b,
     archiveprefix = {arXiv},
     arxivid = {1911.09117},
     author = {Zhang, Shi-Xin and Wan, Zhou-Quan and Yao, Hong},
     doi = {10.1103/PhysRevResearch.5.033041},
     eprint = {1911.09117},
     issn = {2643-1564},
     journal = {Phys. Rev. Res.},
     month = jul,
     number = {3},
     pages = {033041},
     title = {{Automatic differentiable Monte Carlo: Theory and application}},
     url = {https://link.aps.org/doi/10.1103/PhysRevResearch.5.033041},
     volume = {5},
     year = {2023},
   }

3. PRL

   Discrete Time Crystal Enabled by Stark Many-Body Localization

   Shuo Liu, Shi-Xin Zhang^†, Chang-Yu Hsieh , Shengyu Zhang, and Hong Yao^†

   Phys. Rev. Lett., Mar 2023

   Abs Bib HTML PDF

   Discrete time crystal (DTC) has recently attracted increasing attention, but most DTC models and their properties are only revealed after disorder average. In this Letter, we propose a simple disorder-free periodically driven model that exhibits nontrivial DTC order stabilized by Stark many-body localization (MBL). We demonstrate the existence of DTC phase by analytical analysis from perturbation theory and convincing numerical evidence from observable dynamics. The new DTC model paves a new promising way for further experiments and deepens our understanding of DTC. Since the DTC order doesn’t require special quantum state preparation and the strong disorder average, it can be naturally realized on the noisy intermediate-scale quantum (NISQ) hardware with much fewer resources and repetitions. Moreover, besides the robust subharmonic response, there are other novel robust beating oscillations in Stark-MBL DTC phase which are absent in random or quasi-periodic MBL DTC.

   @article{Liu2022_DTC,
     archiveprefix = {arXiv},
     arxivid = {2208.02866},
     author = {Liu, Shuo and Zhang, Shi-Xin and Hsieh, Chang-Yu and Zhang, Shengyu and Yao, Hong},
     doi = {10.1103/PhysRevLett.130.120403},
     eprint = {2208.02866},
     issn = {0031-9007},
     journal = {Phys. Rev. Lett.},
     month = mar,
     number = {12},
     pages = {120403},
     title = {{Discrete Time Crystal Enabled by Stark Many-Body Localization}},
     url = {https://link.aps.org/doi/10.1103/PhysRevLett.130.120403},
     volume = {130},
     year = {2023},
   }

4. Quantum

   TensorCircuit: a Quantum Software Framework for the NISQ Era

   Shi-Xin Zhang, Jonathan Allcock, Zhou-Quan Wan, Shuo Liu, Jiace Sun, Hao Yu, and 10 more authors

   Quantum, Feb 2023

   Abs Bib HTML PDF

   TensorCircuit is an open source quantum circuit simulator based on tensor network contraction, designed for speed, flexibility and code efficiency. Written purely in Python, and built on top of industry-standard machine learning frameworks, TensorCircuit supports automatic differentiation, just-in-time compilation, vectorized parallelism and hardware acceleration. These features allow TensorCircuit to simulate larger and more complex quantum circuits than existing simulators, and are especially suited to variational algorithms based on parameterized quantum circuits. TensorCircuit enables orders of magnitude speedup for various quantum simulation tasks compared to other common quantum software, and can simulate up to 600 qubits with moderate circuit depth and low-dimensional connectivity. With its time and space efficiency, flexible and extensible architecture and compact, user-friendly API, TensorCircuit has been built to facilitate the design, simulation and analysis of quantum algorithms in the Noisy Intermediate-Scale Quantum (NISQ) era.

   @article{Zhang2022_tc,
     archiveprefix = {arXiv},
     arxivid = {2205.10091},
     author = {Zhang, Shi-Xin and Allcock, Jonathan and Wan, Zhou-Quan and Liu, Shuo and Sun, Jiace and Yu, Hao and Yang, Xing-Han and Qiu, Jiezhong and Ye, Zhaofeng and Chen, Yu-Qin and Lee, Chee-Kong and Zheng, Yi-Cong and Jian, Shao-Kai and Yao, Hong and Hsieh, Chang-Yu and Zhang, Shengyu},
     doi = {10.22331/q-2023-02-02-912},
     eprint = {2205.10091},
     issn = {2521-327X},
     journal = {Quantum},
     month = feb,
     pages = {912},
     title = {{TensorCircuit: a Quantum Software Framework for the NISQ Era}},
     url = {https://quantum-journal.org/papers/q-2023-02-02-912/},
     volume = {7},
     year = {2023},
   }

5. PRB

   Probing many-body localization by excited-state variational quantum eigensolver

   Shuo Liu, Shi-Xin Zhang^†, Chang-Yu Hsieh^† , Shengyu Zhang, and Hong Yao^†

   Phys. Rev. B, Jan 2023

   Abs Bib HTML PDF

   Non-equilibrium physics including many-body localization (MBL) has attracted increasing attentions, but theoretical approaches of reliably studying non-equilibrium properties remain quite limited. In this Letter, we propose a systematic approach to probe MBL phases via the excited-state variational quantum eigensolver (VQE) and demonstrate convincing results of MBL on a quantum hardware, which we believe paves a promising way for future simulations of non-equilibrium systems beyond the reach of classical computations in the noisy intermediate-scale quantum (NISQ) era. Moreover, the MBL probing protocol based on excited-state VQE is NISQ-friendly, as it can successfully differentiate the MBL phase from thermal phases with relatively-shallow quantum circuits, and it is also robust against the effect of quantum noises.

   @article{Liu2023_VQEX,
     archiveprefix = {arXiv},
     arxivid = {2111.13719},
     author = {Liu, Shuo and Zhang, Shi-Xin and Hsieh, Chang-Yu and Zhang, Shengyu and Yao, Hong},
     doi = {10.1103/PhysRevB.107.024204},
     eprint = {2111.13719},
     issn = {2469-9950},
     journal = {Phys. Rev. B},
     month = jan,
     number = {2},
     pages = {024204},
     title = {{Probing many-body localization by excited-state variational quantum eigensolver}},
     url = {https://link.aps.org/doi/10.1103/PhysRevB.107.024204},
     volume = {107},
     year = {2023},
   }

2022

1. PRB

   Mitigating the fermion sign problem by automatic differentiation

   Zhou-Quan Wan, Shi-Xin Zhang^†, and Hong Yao^†

   Phys. Rev. B, Dec 2022

   Abs Bib HTML PDF

   As an intrinsically unbiased method, the quantum Monte Carlo (QMC) method is of unique importance in simulating interacting quantum systems. Although the QMC method often suffers from the notorious sign problem, the sign problem of quantum models may be mitigated by finding better choices of the simulation scheme. However, a general framework for identifying optimal QMC schemes has been lacking. Here, we propose a general framework using automatic differentiation to automatically search for the best QMC scheme within a given ansatz of the Hubbard-Stratonovich transformation, which we call "automatic differentiable sign optimization" (ADSO). We apply the ADSO framework to the honeycomb lattice Hubbard model with Rashba spin-orbit coupling and demonstrate that ADSO is remarkably effective in mitigating and even solving its sign problem. Specifically, ADSO finds a sign-free point in the model which was previously thought to be sign-problematic. For the sign-free model discovered by ADSO, its ground state is shown by sign-free QMC simulations to possess spiral magnetic ordering; we also obtained the critical exponents characterizing the magnetic quantum phase transition.

   @article{Wan2020,
     archiveprefix = {arXiv},
     arxivid = {2010.01141},
     author = {Wan, Zhou-Quan and Zhang, Shi-Xin and Yao, Hong},
     doi = {10.1103/PhysRevB.106.L241109},
     eprint = {2010.01141},
     issn = {2469-9950},
     journal = {Phys. Rev. B},
     month = dec,
     number = {24},
     pages = {L241109},
     title = {{Mitigating the fermion sign problem by automatic differentiation}},
     url = {https://link.aps.org/doi/10.1103/PhysRevB.106.L241109},
     volume = {106},
     year = {2022},
   }

2. QST

   Differentiable quantum architecture search

   Shi-Xin Zhang, Chang-Yu Hsieh^† , Shengyu Zhang, and Hong Yao^†

   Quantum Science and Technology, Oct 2022

   Abs Bib HTML PDF

   Quantum architecture search (QAS) is the process of automating architecture engineering of quantum circuits. It has been desired to construct a powerful and general QAS platform which can significantly accelerate current efforts to identify quantum advantages of error-prone and depth-limited quantum circuits in the NISQ era. Hereby, we propose a general framework of differentiable quantum architecture search (DQAS), which enables automated designs of quantum circuits in an end-to-end differentiable fashion. We present several examples of circuit design problems to demonstrate the power of DQAS. For instance, unitary operations are decomposed into quantum gates, noisy circuits are re-designed to improve accuracy, and circuit layouts for quantum approximation optimization algorithm are automatically discovered and upgraded for combinatorial optimization problems. These results not only manifest the vast potential of DQAS being an essential tool for the NISQ application developments, but also present an interesting research topic from the theoretical perspective as it draws inspirations from the newly emerging interdisciplinary paradigms of differentiable programming, probabilistic programming, and quantum programming.

   @article{Zhang2020_DQAS,
     archiveprefix = {arXiv},
     arxivid = {2010.08561},
     author = {Zhang, Shi-Xin and Hsieh, Chang-Yu and Zhang, Shengyu and Yao, Hong},
     doi = {10.1088/2058-9565/ac87cd},
     eprint = {2010.08561},
     issn = {2058-9565},
     journal = {Quantum Science and Technology},
     month = oct,
     number = {4},
     pages = {045023},
     title = {{Differentiable quantum architecture search}},
     url = {https://iopscience.iop.org/article/10.1088/2058-9565/ac87cd},
     volume = {7},
     year = {2022},
   }

3. PRL

   

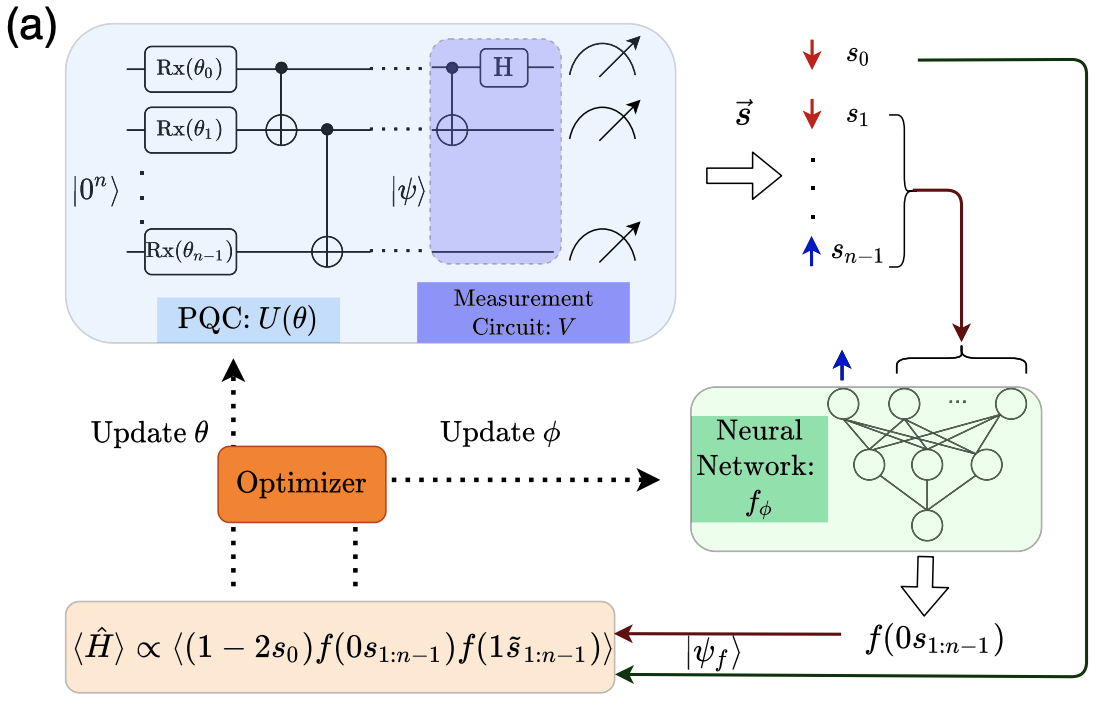   Variational Quantum-Neural Hybrid Eigensolver

   Shi-Xin Zhang, Zhou-Quan Wan, Chee-Kong Lee, Chang-Yu Hsieh^† , Shengyu Zhang, and Hong Yao^†

   Phys. Rev. Lett., Mar 2022

   Abs Bib HTML PDF

   The variational quantum eigensolver (VQE) is one of the most representative quantum algorithms in the noisy intermediate-size quantum (NISQ) era, and is generally speculated to deliver one of the first quantum advantages for the ground-state simulations of some non-trivial Hamiltonians. However, short quantum coherence time and limited availability of quantum hardware resources in the NISQ hardware strongly restrain the capacity and expressiveness of VQEs. In this Letter, we introduce the variational quantum-neural hybrid eigensolver (VQNHE) in which the shallow-circuit quantum ansatz can be further enhanced by classical post-processing with neural networks. We show that VQNHE consistently and significantly outperforms VQE in simulating ground-state energies of quantum spins and molecules given the same amount of quantum resources. More importantly, we demonstrate that for arbitrary post-processing neural functions, VQNHE only incurs an polynomial overhead of processing time and represents the first scalable method to exponentially accelerate VQE with non-unitary post-processing that can be efficiently implemented in the NISQ era.

   @article{Zhang2021_VQNHE,
     archiveprefix = {arXiv},
     arxivid = {2106.05105},
     author = {Zhang, Shi-Xin and Wan, Zhou-Quan and Lee, Chee-Kong and Hsieh, Chang-Yu and Zhang, Shengyu and Yao, Hong},
     doi = {10.1103/PhysRevLett.128.120502},
     eprint = {2106.05105},
     issn = {0031-9007},
     journal = {Phys. Rev. Lett.},
     month = mar,
     number = {12},
     pages = {120502},
     title = {{Variational Quantum-Neural Hybrid Eigensolver}},
     url = {https://link.aps.org/doi/10.1103/PhysRevLett.128.120502},
     volume = {128},
     year = {2022},
   }

2021

1. MLST

   

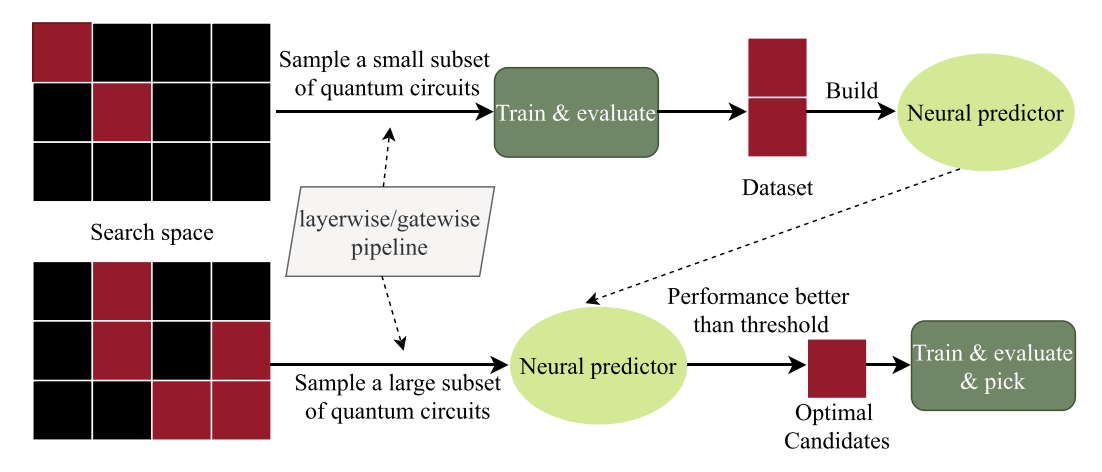   Neural predictor based quantum architecture search

   Shi-Xin Zhang, Chang-Yu Hsieh^† , Shengyu Zhang, and Hong Yao^†

   Machine Learning: Science and Technology, Dec 2021

   Abs Bib HTML PDF

   Variational quantum algorithms (VQAs) are widely speculated to deliver quantum advantages for practical problems under the quantum–classical hybrid computational paradigm in the near term. Both theoretical and practical developments of VQAs share many similarities with those of deep learning. For instance, a key component of VQAs is the design of task-dependent parameterized quantum circuits (PQCs) as in the case of designing a good neural architecture in deep learning. Partly inspired by the recent success of AutoML and neural architecture search (NAS), quantum architecture search (QAS) is a collection of methods devised to engineer an optimal task-specific PQC. It has been proven that QAS-designed VQAs can outperform expert-crafted VQAs in various scenarios. In this work, we propose to use a neural network based predictor as the evaluation policy for QAS. We demonstrate a neural predictor guided QAS can discover powerful quantum circuit ansatz, yielding state-of-the-art results for various examples from quantum simulation and quantum machine learning. Notably, neural predictor guided QAS provides a better solution than that by the random-search baseline while using an order of magnitude less of circuit evaluations. Moreover, the predictor for QAS as well as the optimal ansatz found by QAS can both be transferred and generalized to address similar problems.

   @article{Zhang2021_neural,
     author = {Zhang, Shi-Xin and Hsieh, Chang-Yu and Zhang, Shengyu and Yao, Hong},
     doi = {10.1088/2632-2153/ac28dd},
     issn = {2632-2153},
     journal = {Machine Learning: Science and Technology},
     month = dec,
     number = {4},
     pages = {045027},
     title = {{Neural predictor based quantum architecture search}},
     url = {https://iopscience.iop.org/article/10.1088/2632-2153/ac28dd},
     volume = {2},
     year = {2021},
   }

2018

1. PRL

   Universal Properties of Many-Body Localization Transitions in Quasiperiodic Systems

   Shi-Xin Zhang, and Hong Yao^†

   Phys. Rev. Lett., Dec 2018

   Abs Bib HTML PDF

   Precise nature of MBL transitions in both random and quasiperiodic (QP) systems remains elusive so far. In particular, whether MBL transitions in QP and random systems belong to the same universality class or two distinct ones has not been decisively resolved. Here we investigate MBL transitions in one-dimensional (d\!=\!1) QP systems as well as in random systems by state-of-the-art real-space renormalization group (RG) calculation. Our real-space RG shows that MBL transitions in 1D QP systems are characterized by the critical exponent ν\!≈\!2.4, which respects the Harris-Luck bound (ν\!>\!1/d) for QP systems. Note that ν\!≈\! 2.4 for QP systems also satisfies the Harris-CCFS bound (ν\!>\!2/d) for random systems, which implies that MBL transitions in 1D QP systems are stable against weak quenched disorder since randomness is Harris irrelevant at the transition. We shall briefly discuss experimental means to measure νof QP-induced MBL transitions.

   @article{Zhang2018_MBL,
     archiveprefix = {arXiv},
     arxivid = {1805.05958},
     author = {Zhang, Shi-Xin and Yao, Hong},
     doi = {10.1103/PhysRevLett.121.206601},
     eprint = {1805.05958},
     issn = {10797114},
     journal = {Phys. Rev. Lett.},
     number = {20},
     pages = {206601},
     publisher = {American Physical Society},
     title = {{Universal Properties of Many-Body Localization Transitions in Quasiperiodic Systems}},
     url = {https://doi.org/10.1103/PhysRevLett.121.206601},
     volume = {121},
     year = {2018},
   }