Prof. Shi-Xin Zhang

Shi-Xin Zhang (张士欣)
Principal Investigator
Associate Professor
Institue of Physics
Chinese Academy of Sciences
shixinzhang@iphy.ac.cn
zhangshixin
0000-0003-0347-9750
refraction-ray
official page
https://re-ra.xyz
Shi-Xin Zhang (张士欣)
Beijing, China
See my academic CV here.
Experience
-
2024 - now, Institute of Physics, Chinese Academy of Sciences, Associate Professor
-
2021 - 2024, Tencent Quantum Laboratory, Senior Research Scientist
Education
-
2016 - 2021, Institue for Advanced Study, Tsinghua University, PhD in Physics
-
2012 - 2016, Department of Physics, Tsinghua University, BSc in Physics
Achievements
Quantum Software
Created and developed TensorCircuit and TensorCircuit-NG:
-
An open-source, high-performance quantum software that provides a unified interface and infrastructure for quantum programming, enabling the seamless integration of tensor networks, neural networks, and quantum circuits
-
Built upon modern machine learning frameworks including TensorFlow, Jax, and PyTorch, and features an advanced tensor network contraction engine.
-
Offers comprehensive solutions for hybrid CPU-GPU-QPU and distributed computing.
-
Widely adopted by universities, research institutes, and companies worldwide, with over 140 citations, including from research teams at Google, NVIDIA, IBM, and leading academic groups at Harvard, Caltech, and Chicago.
-
Selected as one of the “Top 10 Influential Events in 2022” by QuantumChina.
-
The only quantum software as the baseline for NVIDIA’s cuQuantum in its release.
Quantum Algorithms
-
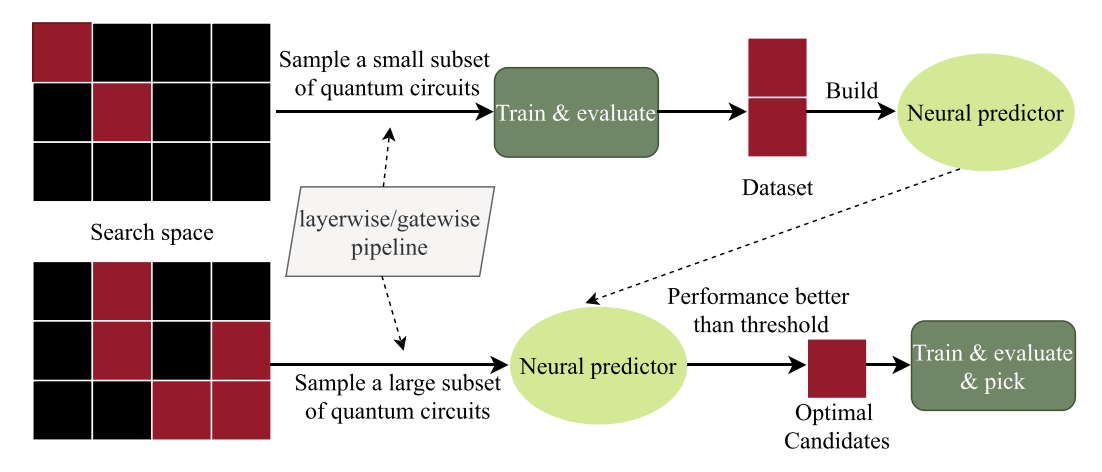
Pioneered the concept and terminology of Quantum Architecture Search (QAS). This work inspired the emergence of the field and established new paradigms for automated quantum circuit design. A search for “Quantum Architecture Search” on Google Scholar yields over 500 academic papers.
-
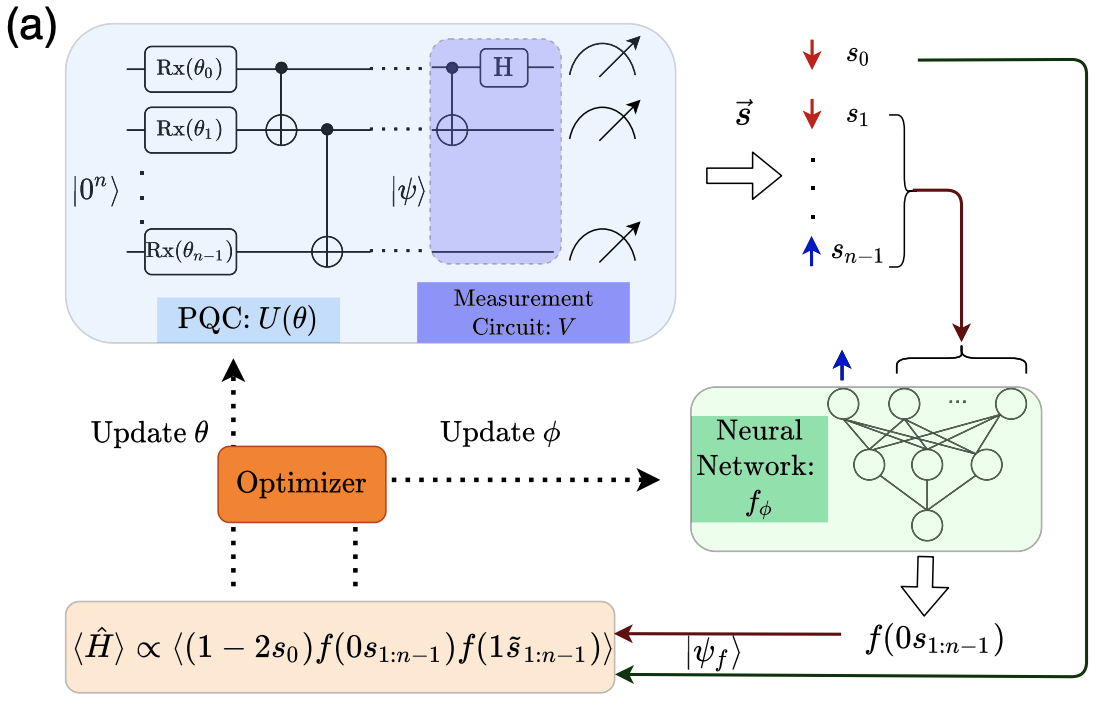
Developed a hybrid wavefunction ansatz that efficiently fuses quantum circuits with neural networks. This approach significantly boosts the model’s expressive power and achieves an exponential speedup over non-unitary methods proposed by IBM’s team.
Non-Equilibrium Quantum Physics
-
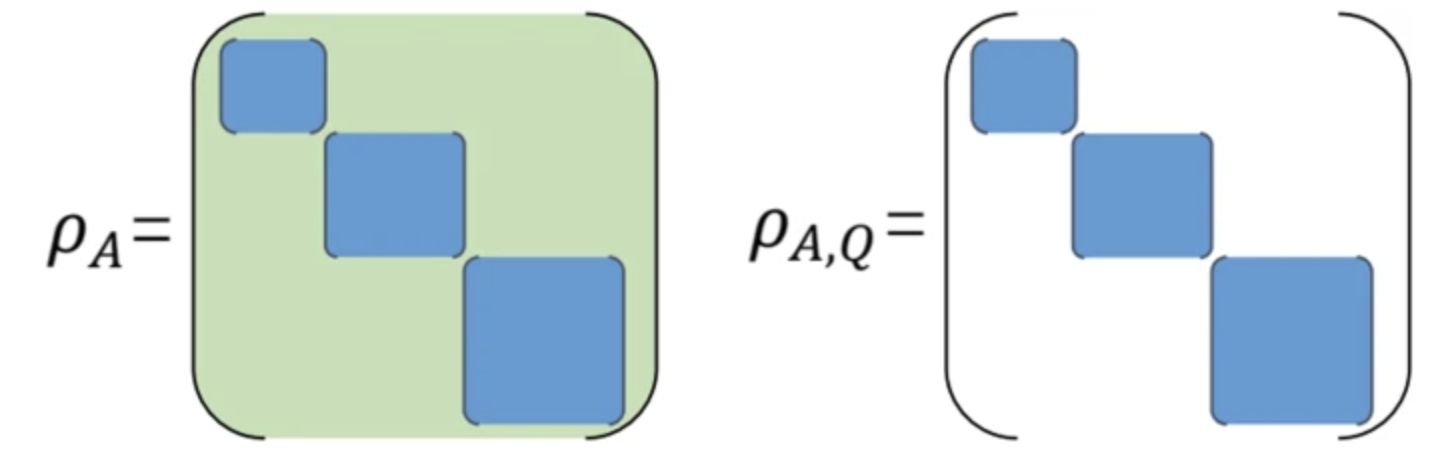
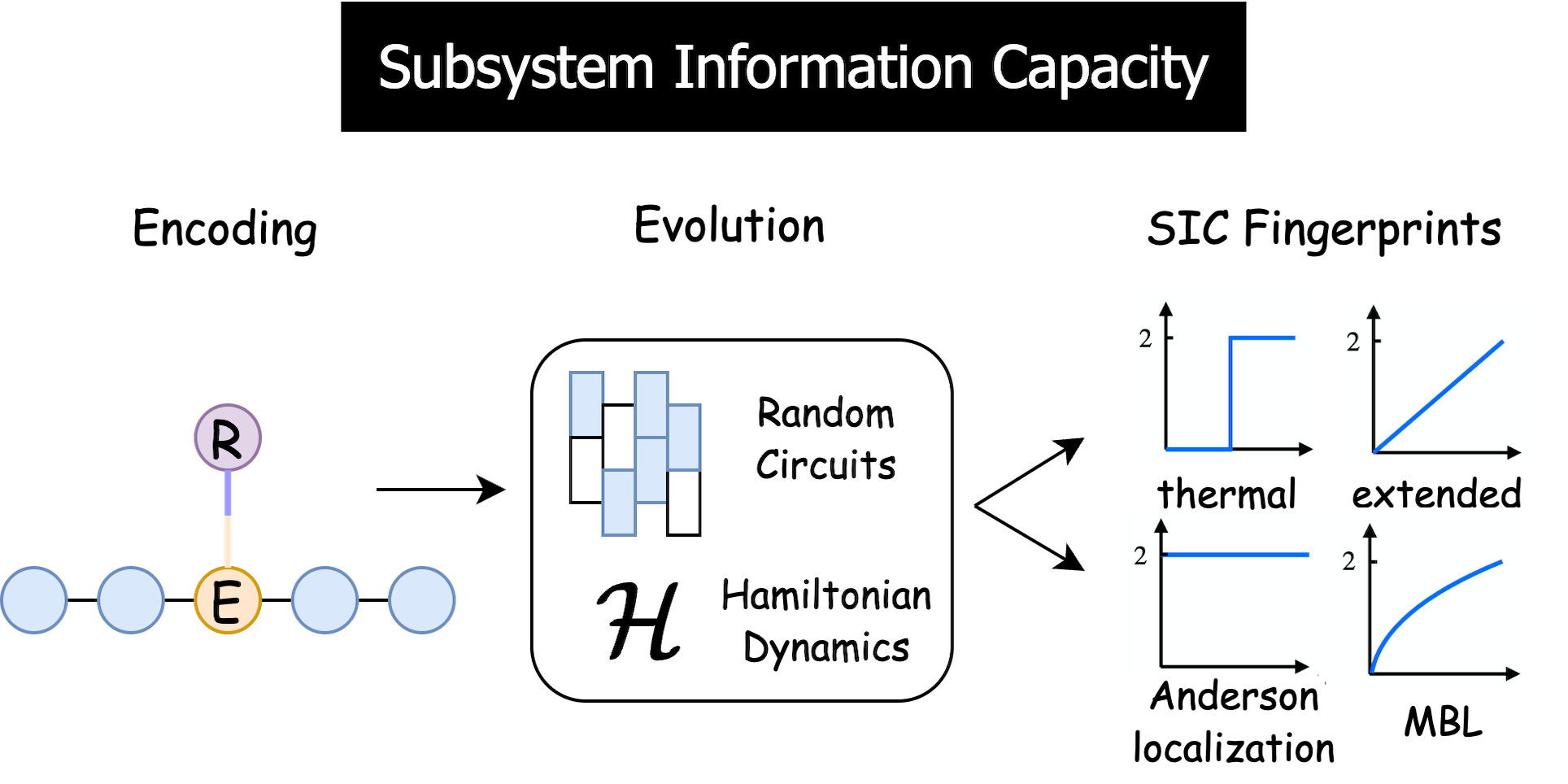
Developed the theory of the quasiperiodic many-body localized (MBL) phase and phase transitions. Performed the first large-scale simulation to determine the universality class of the critical behavior in quasiperiodic MBL, establishing its robustness against random disorder.
-
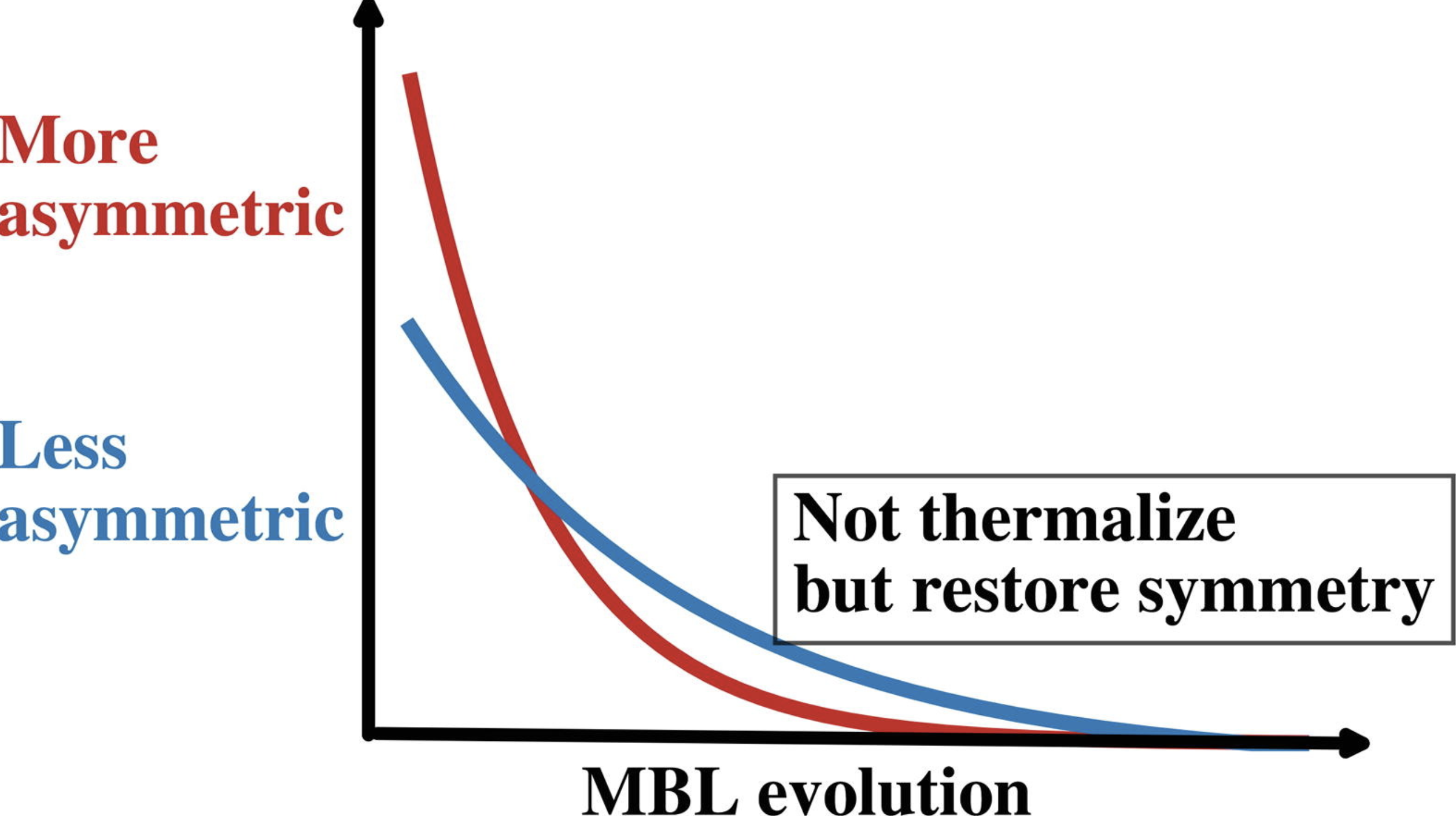
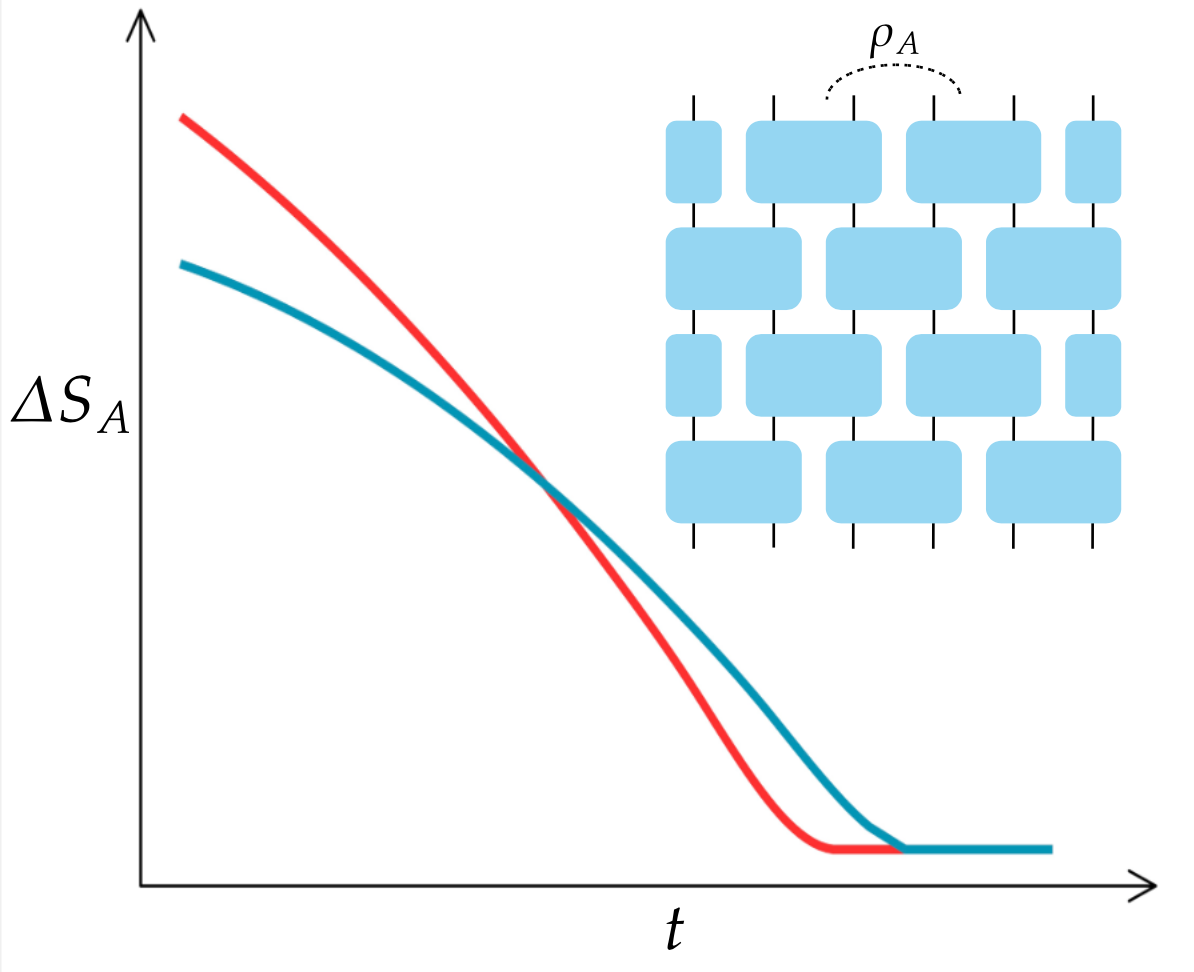
Conducted the first investigation of the quantum Mpemba Effect in both thermalized and MBL systems, proposing a general physical mechanism for its occurrence in generic quantum many-body systems. Pioneered the study of the Mpemba effect in the context of SU(2) symmetry, symmetry-breaking dynamics, and imaginary-time evolution, significantly impacting the field and substantially broadening the scope of Mpemba effect.
-
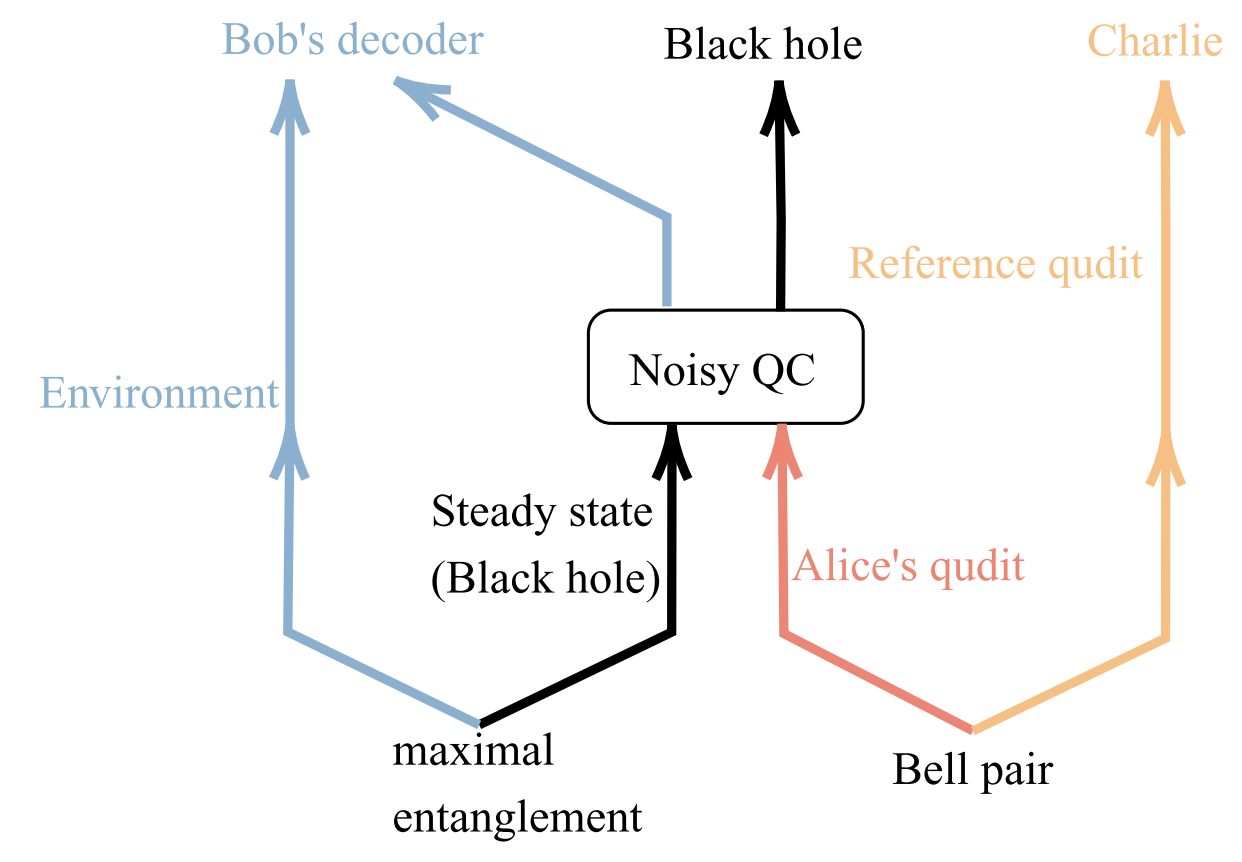
Systematically investigated the interplay between random unitary evolution, measurement, and noise, with the work being cited by Google’s experimental paper in Nature.
Differentiable Programming
-
Extended the paradigm of differentiable programming to a broader range of operators and workflows in quantum physics. Theoretically derived the gradients for the complex-valued singular value decomposition and contributed the implementation to TensorFlow.
-
My Ph.D. thesis, “Differentiable Programming in Quantum Physics,” was awarded the Tsinghua University Excellent Doctoral Dissertation Award.
Open Source
Patents
Applied for over 30 domestic and international patents focusing on key technologies in quantum computing.
Publications
50+ journal papers and eprints inluding 6 Physical Review Letters. 1300+ citations, H-index:20.